Obecná teorie relativity přinesla rozšíření elektromagnetické teorie světla na oblast, kde do úvahy přichází působení gravitačních sil. Zákony teorie elektromagnetického pole, včetně Maxwellových rovnic, jsou totiž odvozovány pro vakuum při zanedbání gravitačního pole. V porovnání s elektromagnetickými silami jsou gravitační síly velmi malé a v běžných pozemských podmínkách jejich vliv je nepozorovatelný. Jiná je situace v kosmických prostorech, kde obrovská hmotnost hvězd, včetně našeho Slunce, svou gravitací ovlivňuje přímočaré šíření světla.

Na základě své obecné teorie relativity Einstein předpověděl posuv pozorované polohy hvězd vlivem gravitačního pole Slunce. Důkaz správnosti této teorie podaly astronomické záznamy pořízené dne 29. května 1919 při zatmění Slunce v Sobralu (v Brazílii) a na ostrově Principe (u pobřeží západní Afriky). Astronomical Royal Society pozorováním a fotografickým zdokumentováním tohoto úkazu pověřila několik svých nejlepších astronomů (Eddingtona, Crommelina a Davidsona) a vypravila na uvedena místa dvě expedice ([1] str. 175). Úkaz zatmění Slunce popíšeme pomocí Obr. 1.

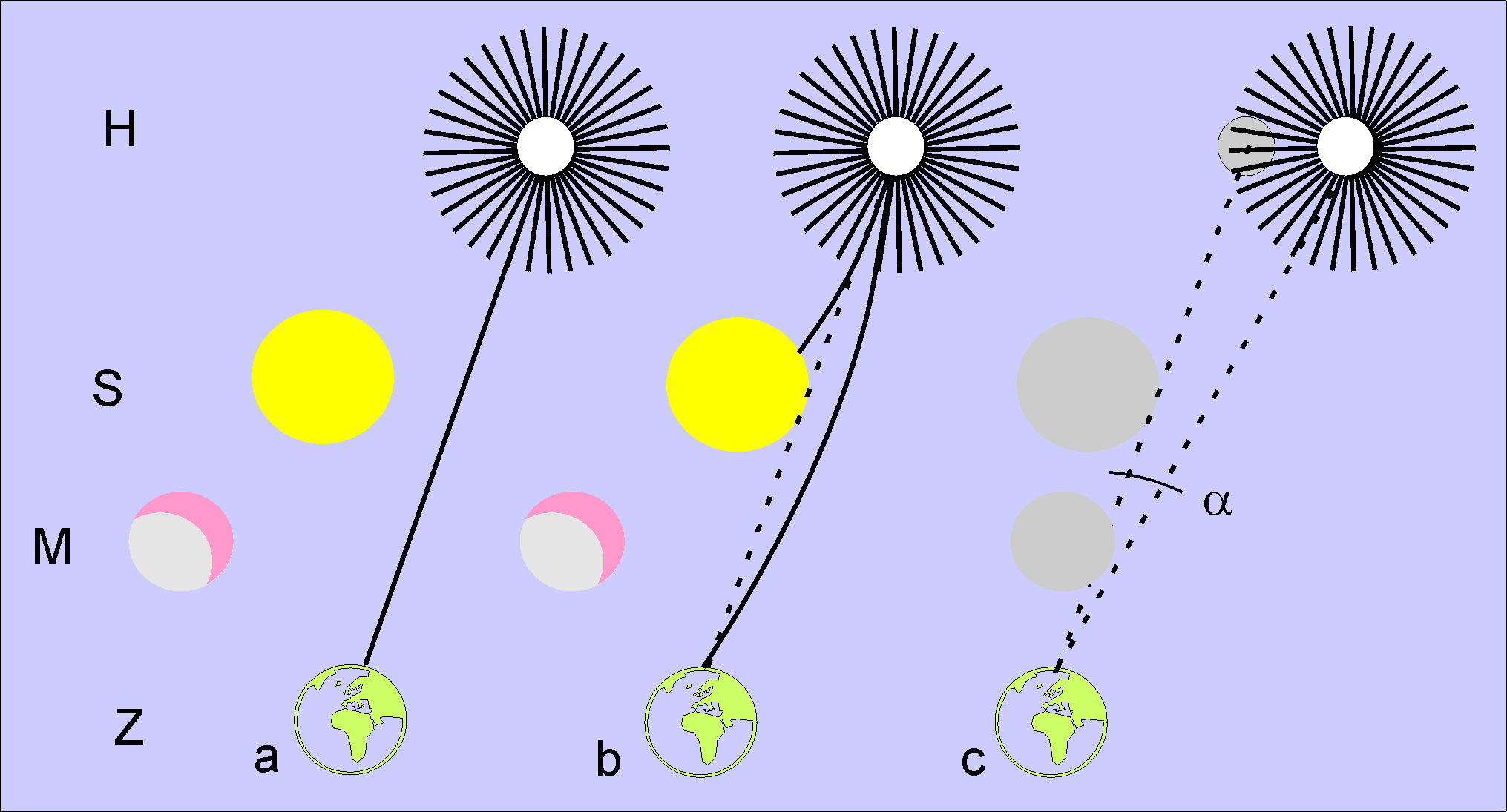
Obr. 1. Zatmění Slunce

Na noční obloze svítí hvězda, která své paprsky vysílá všemi směry. „Jeden“ paprsek dosáhne až k nám na Zemi díky tomu, že Slunce mu nestojí v cestě (Obr. 1a). Když se Slunce postaví paprsku do cesty (Obr. 1b), tento paprsek již na Zemi nemůže dorazit. Věc ještě není ztracená, jelikož jiný paprsek dosáhne na Zemi, který se ohýbá díky gravitačním silám Slunce. Pro velké osvětlení Sluncem hvězdu ze Země nelze pozorovat. Zakryje-li Slunce Měsíc, nastane úplné zatmění Slunce, které nyní umožňuje hvězdu pozorovat (Obr. 1c). Tento neběsný úkaz nastal 29. května 1919 na zmíněných místech v Brazílii a Africe a umožnil pořídit fotografické snímky, které potvrdily Einsteinovu předpověď o úchylce pozorování hvězdy o úhel α = 0,00049 stupňů. Pod takovým úhlem bychom viděli předmět o velikosti jednoho metru ze vzdálenosti asi 110 kilometrů.

Světlo dalo podnět k vzniku obecné teorie relativity. Světlo nám přináší informace o daleké a blízké vzdálenosti v prostoru. Ale co to vlastně světlo je? Odpověď na tuto otázku se měnila po staletích.

Newton (1643–1727) ve své knize z r. 1704 učil, že světlo je proud korpuskulí (částic). Co pod těmito částicemi myslel, to nenapsal. Užitečná představa je, že jsou to drobné a pružné tenisové míčky, kterými lze názorně přiblížit postuláty a zákony geometrické optiky, která je teorii mnoha optických přístrojů: světlo se šíří přímočaře jako by letěl míček, kdyby nebyla gravitace Země, světlo se odráží od zrcadla stejně tak jako míček: úhel dopadu se rovná úhlu odrazu. Jenže už i samotný Newton měl potíže objasnit barvu světla, nemluvě už o jeho interferenci .

Posledně jmenované jevy vysvětluje vlnová teorie světla, kterou navrhl Huyghens (1629-1695) ve své knize v r. 1690. Jeho teorie však byla zastíněna autoritou Newtona až do začátku 19. století. Zájem o vlnovou teorii oživil Young (1773-1829) jehož dvojštěrbinový experiment (publikovaný v r. 1803) se dodnes uvádí jako úvod k výuce o světle. Jenže co se vlní, když je světlo? Odpověď byla po ruce: vlní se éter. Potíž byla v tom, že bádání o podstatě éteru trvalo již od nepaměti bez úspěchu.

První smrtící ránu éteru nasadili Faraday (1791-1867) a Maxwell (1831-1879) svou teorii elektromagnetického pole. Podle této teorie světlo je vlnění elektromagnetického pole. Existenci elektromagnetických vln Maxwell předpověděl v roce 1863. Svými pokusy prováděnými v letech 1887-1888 to potvrdil Herz (1857-1894). Definitivní smrtící ránu ovšem éteru nasadili Michelson (1852-1921) a Morley (1838-1923) svými experimenty (1887) se šířením rychlosti světla v závislosti na rychlosti Země kolem Slunce, které ukázaly, že rychlost světla nezávisí na rychlosti Země.

Závěry Faradayově-Maxwellově teorie a uvedena měření Michelsona-Morleye posloužily Einsteinovi (1879-1955) jako pádný argument k vytvoření speciální teorii relativity (1905), která se zabývá transformací souřadnic prostoru a času ve vztažných soustavách, která se vzájemně pohybují přímočaře konstantní rychlostí. Postulátem speciální teorie relativity je, že světlo se ve vakuu šíří rychlostí co, kterou nemůže překonat (dosáhnout) žádný jiný objekt. Přitom se mlčky předpokládá, že se jedná o tvrzení platné pro prostředí, kde nepůsobí gravitace.

V roce 1900 Planck (1858-1947) objevil, že černé těleso vyzařuje světlo po malých dávkách – kvantech. Einstein pak v roce 1905 vysvětlil fotoefekt pomocí těchto kvant energie a nazval je fotony. To jsou počátky kvantové elektrodynamiky (QED), kde světlo se považuje za proudění fotonů, čím se velkým obloukem vracíme k Newtonově korpuskulární teorii. Teorii světla podle QED zpřístupnil široké veřejnosti Feynman (1918-1988) svou populární knihou [2].

Jako i jiné mikročástice, foton také se v jistých situacích projevuje jako korpuskule (fotoefekt), v jiných jevech (interference [2]) je to spíš vlna. V stávající animaci zakřivení časoprostoru budeme s ním zacházet jako s korpuskulí.

Zde formulujeme pravidla chování fotonu pro potřeby analýzy jeho pohybu vlivem gravitačního pole. Omezíme se přitom na pole Slunce, nebo na jiné nebeské těleso – černou díru. Pro obě tělesa předpokládáme, že mají kulový tvar o hmotnosti M.

Foton je definovaný svou energii W_f = hf, kde h = 6,6×10^-34 [Js] je Planckova konstanta a f je kmitočet světla. Energii W_f říkáme vlastní energie, jelikož v gravitačním poli má foton také potenciální (gravitační) Wp a kinetickou energii Wk.

Mezi energii E a hmotností m platí proslulá Einsteinova rovnice E = mc_o², kde c_o je rychlost světla ve vakuu – v tomto případě je to však jen převodní koeficient mezi energii a hmotností, podobně jako Planckova konstanta h je převodní koeficient mezi energii a kmitočtem. Pod proměnnou E je třeba rozumět celkovou energii fotonu E = W_f + Wp + Wk. Respektujeme zákon zachování energie, tudíž celková energie E je konstanta a teda i hmotnost m fotonu podél celého jeho letu je beze změn.

V našem animačním programu se omezujeme na analýzu zakřivení trajektorie a času fotonu v gravitačním poli Slunce a černé díry. Jsou to tělesa kulového tvaru o hmotnosti M, ovšem rozdílné velikosti. Potenciální energie hmotnosti m v jejich poli je Wp = –gMm/r, kde g = 6.67×10^-11 [m3kg-1s^-2] je gravitační konstanta a r je vzdálenost fotonu do centra hmotnosti M. Podstatné je, že potenciální energie fotonu je vždy záporná a teda je tím větší (blíž k nule) čím je foton dál od hmotnosti M (Slunce). Foton při svém letu v gravitačním poli mění vlastní energii na potenciální a naopak.

Uvedený výraz pro potenciální energii vyplývá z Newtonova gravitačního zákona F = gMmr/r³ , kde F je vektor přitažlivé síly působící na hmotnost m a r je vektor vzdálenosti fotonu k centru hmotnosti M. Tato sila uděluje fotonu zrychlení a ve směru hmotnosti M podle Newtonova zákona o síle F = ma. Díky tomuto zrychlení, za elementární dobu Δt foton nabude rychlost Cg = aΔt a urazí dráhu délky ΔSg = a(Δt)²/2, přičem Δt je čas měřený hodinami na Zemi. Má-li foton rychlost Cs na začátku časového úseku Δt, pak na jeho konci bude jeho rychlost Cs + Cg (vektorový součet) a foton se posune o ΔSg směrem k centru hmotnosti M (Obr. 3).

Vlivem gravitace se rychlost fotonu při jeho letu mění a může nabýt větší nebo menší rychlost než je c_o. Einsteinova speciální teorie relativity je postavena na postulátu konstantní rychlosti světla c_o ve vakuu jako o nejvyšší rychlosti, kterou lze dosáhnout. Nicméně Einstein ve své knize ([1] str. 165 a 136) píše: „…často již zmíněný zákon o konstantnosti rychlosti světla ve vakuu, který tvoří jeden ze základních předpokladů speciální theorie relativity, podle obecné theorie relativity nemá neomezenou platnost“, a dále pokračuje: „Dá se pouze souditi, že speciální teorii relativity nikterak nenáleží neomezený obor platnosti; její výsledky platí jen potud, pokud nemusíme přihlížeti k vlivům gravitačního pole na jevy (na př. na světlo)“. Jinými slovy, v gravitačním poli foton může letět rychlostí c odlišnou (větší, nebo menší) než je c_o, kterou na Zemi naměříme ve vakuu (v těchto úvahách Země má zanedbatelnou gravitaci). Jelikož má foton hmotnost m, jeho kinetická energie je Wk = mc²/2. Během svého letu se foton nachází v gravitačním poli různé intenzity, čím se mění jeho potenciální energie. To má za následek odpovídající změnu vlastní a kinetické energie fotonu. Variace těchto tří forem energie je omezena nulovým součtem jejich elementárních změn. Odtud pro elementární změnu potenciální energie vyplývá ΔWp = -(ΔW_f + ΔWk). Je to vyjádření potenciální energie výhradně dynamickými pojmy na rozdíl od výše uvedeného gravitačního výrazu.

Souhrnem lze říct, že let fotonu prostorem je doprovázen vzájemnou výměnou tří forem jeho energie.

1. Potenciální energie, která má svůj původ v gravitačním poli.
2. Vlastní energie, čili kvantum elektromagnetického záření.
3. Kinetická energie, která je úměrná kvadrátu rychlosti fotonu.

Přitom v každé poloze fotonu podél jeho trasy se proměny energií řídí principem neměnnosti součtu všech tří forem energie: ΔW_f + ΔWp + ΔWk = 0. Na těchto základech je vyvinutý animační program, který je uveden v dalším článku (Obr 2).

Foton nikdo „neviděl“, vnímáme jen jeho působení při dopadu na sítnici oka. V povaze myšlení člověka je přiřadit neviditelným přírodním aktérům objekty, které jsou nám dobře známy z každodenního života. Feynman ve své knize [2] mluví o fotonu jako o hodinách, jejichž jediná ručička rotuje frekvencí f. Jsou to hodiny fotonu, jejichž chod budeme porovnávat s chodem hodin na Zemi při výkladu zakřivení času.

Dnes platnou jednotkou času v soustavě SI (Système International d’Unités) pro pozemské hodiny je sekunda stanovena podle následující definice: Sekunda je doba trvání 9 192 631 770 period záření, které odpovídá přechodu mezi dvěma hladinami velmi jemné struktury základního stavu atomu cesia 133. Měrná jednotka času je tak definovaná kmitočtem světla. Není to poslední formulace jednotky času, neboť se připravuje nová, která upřesňuje podmínky definice [3], avšak počet period záření nadále zůstává beze změn. V následujících článcích předpokládáme, že hodiny fotonu jsou téže „konstrukce“ jako pozemní. Záření atomu cesia při jeho přechodu mezi dvěma hladinami je ovšem ovlivněno gravitačním polem a proto se čas na hodinách fotonu liší od času na pozemních hodinách. V okolí zemského povrchu se chod dokonalých atomových hodin, realizujících výše uvedenou definici sekundy, také mění v závislosti na intenzitě gravitačního pole Země – nadmořské výšky.

Zakřivení časoprostoru ilustruje Obr. 2 tak, jak byl vypočítán programem casoprostor.exe. Gravitační pole hvězdy a Země zanedbáváme – hmotnost Země je nepatrná oproti hmotnosti Slunce a hvězda je příliš daleko. Foton se k Slunci blíží rychlostí světla ve vakuu. Na Obr. 2 vidíme čtyři diagramy, jejichž měřítka mají ilustrativní velikost s cílem zdůraznit daný jev.

• Horní diagram znázorňuje trajektorie fotonů (paprsky světla) při svém letu poté co byly vyslány hvězdou. Jedna trasa končí na Zemi a foton přináší nám správu o existenci hvězdy. Jiné fotony na svých trasách dopadnou na Slunce, nebo nás minou. Přímka kreslená přerušovanou čarou znázorňuje trajektorii, kterou by se foton pohyboval, kdyby ho neovlivňovalo Slunce svým postavením.
• Druhý diagram ukazuje, jak se měnila rychlost letu fotonu, který dopadl na Zemi vlivem gravitace Slunce viděno ze Země a měřeno časem na Zemi. Čárkovaná přímka znázorňuje trasu fotonu letícího konstantní rychlostí, když nepůsobila gravitace Slunce. Hvězda je daleko od slunce a foton se blíží k Slunci z prostředí vakua bez gravitace rychlostí c_o. Při animaci můžeme proto vycházet z toho, že foton touto rychlostí opustil i hvězdu. Jak se blíži k Slunci, které ho přitahuje, jeho rychlost narůstá.V poslední fázi letu se foton vzdaluje od Slunce a jeho rychlost se snižuje opět vlivem přitažlivosti Slunce, ale dřív než dosáhne rychlost c_o dopadne na Zemi. Fotony, které minuli Zemi, pokračují v letu a po gigantické spirálovité dráze by dopadly na Slunce, pokud by je nepohltila nějaká černá díra jak to ilustruje Obr. 8.
• Třetí diagram znázorňuje zrychlení letu fotonu pod působením gravitace Slunce. Po dosažení maximálního zrychlení v blízkosti Slunce, zrychlení začíná klesat a dosáhne nulovou hodnotu. Stane se tak tehdy, když se foton díky své rychlosti pohybuje v konstantní vzdálenosti od Slunce po ekvipotenciále gravitace (Obr. 4). Jakmile se foton začne vzdalovat od Slunce, a vymaňuje se z působení jeho gravitace, let fotonu se zpomaluje, ale jeho rychlost je stále vyšší než c_o jakou se z dálav přiblížil k Slunci.
• Na spodním diagramu (černá křivka) je uveden graf potenciální energie fotonu, který je úměrný reciproké vzdálenosti okamžité polohy fotonu vzhledem k slunci Wp ≈ –1/r. Pokud se zdá podivné, že v blízkosti Slunce se potenciální energie fotonu zmenšuje, pak to není nic mimořádného. S tímto zdánlivě paradoxním tvrzením se spřátelíme, když si uvědomíme, že každý objekt, v tom čísle i foton, má tím menší potenciální energii, čím v silnějším gravitačním poli se nachází. Pozorujeme to a využíváme to také v každodenním životě. Voda v přehradní nádrži má větší potenciální energii než pod přehradou, přestože zde je blíž k centru Země a je přitahována větší silou. Rozdíl potenciálních energii se v hydroelektrárně promění v elektřinu.
• Žlutá křivka na spodním diagramu představuje kinetickou energii Wk vypočítanou jako kvadrát rychlosti fotonu. Červená křivka znázorňuje rozdíl plynutí času hodin fotonu a Země. Hodiny fotonu tikají rychlostí úměrnou jeho kmitočtu f, a tudíž červená křivka zobrazuje také jeho vlastní energii W_f. Je to křivka vyplývající z konstantnosti součtu tří forem energie ΔW_f = –(ΔWp + ΔWk) podle teorie uvedené v článku Foton. Čárkovaná linie představuje nulovou hodnotu (největší možnou) potenciální energii fotonu a současně kinetickou a vlastní energii/kmitočet fotonu když je tento ještě daleko od působení gravitace Slunce.

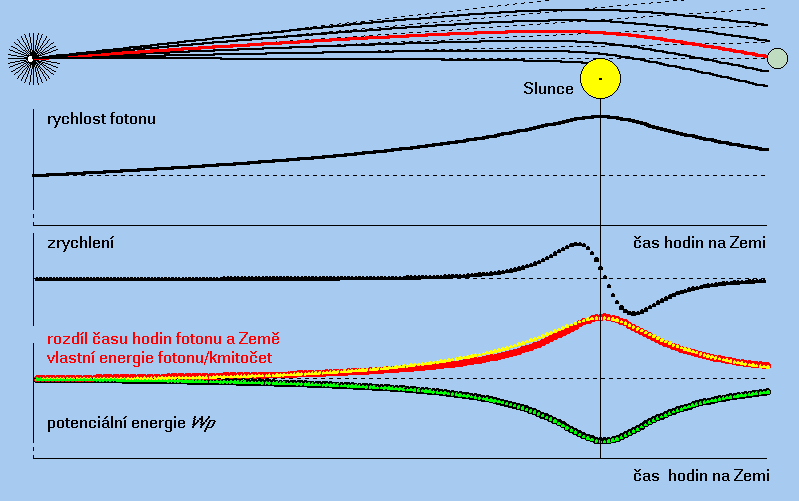
Obr. 2  Animace zakřivení časoprostoru – casoprostor.exe

Pohyb každého objektu se odehrává v čtyřrozměrném prostoru, který lze popsat třemi prostorovými souřadnicemi x, y, z a čtvrtou souřadnici času t. Graf trajektorie na Obr. 2 popisující pohyb fotonu v prostoru je jen průmět dráhy fotonu na rovinu x, y třídimenzionálního grafu Obr. 3, kde třetí rozměr je čas t. Čárkované linie znázorňují grafický postup konstrukci dráhy letu fotonu v časoprostoru. Je to na zakřivené ploše nejkratší spojnice mezi dvěma body , které se říká geodetika. Na ose x a t je rovnoměrná stupnice podle času pozemních hodin. Na ose t je vynesen také průběh času fotonu – přesněji rozdíl času na hodinách fotonu a pozemních.

Obr. 3  Náčrt konstrukce geodetiky – geodetika.exe

Geodetika je trajektorie, pro níž má minimální hodnotu tzv. integrál akce A, který je definován jako časový integrál rozdílu diference kinetické a diference potenciální energie po trase od zdroje k Zemi: A = ∫(ΔWk – Wp)dt = minimum. To znamená, že po každé jiné trase by uvedený integrál měl větší hodnotu. V článku Foton jsme uvedli, že součet diferencí vlastni a gravitační energie, jakožto i součet všech tří forem energie je rovný nule. Z toho lze odvodit, že integrál ∫ΔW_fdt = minimum. Žlutá plocha na Obr. 3 ilustruje tuto minimální hodnotu. Integrální hodnota diferencí vlastní energie fotonu vypovídá, že se frekvence fotonu během jeho letu v gravitačním poli Slunce zvýší o hodnotu úměrnou uvedenému minimu. Znamená to, že na Zemi pozorujeme posunutí spektrálních čar směrem k vyšším frekvencím – tzv. modrý posuv, o kterém bude ještě řeč v dalším článku. Poznamenejme, že stejný integrál akce A vykazuje také geodetika hozeného kamene mezi začátkem a jeho dopadem na Zemi, jelikož se jedná o jeden a ten samý princip dynamiky.

Geodetika na Obr. 3 znázorňuje let fotonu v časoprostorových souřadnicích spojených se Zemi. Můžeme spekulovat, jak vypadá trajektorie znázorněná v souřadnicích spražených s fotonem, který „nepociťuje“ přitažlivou sílu slunce, jelikož ta je vykompenzovaná odstředivou silou pohybu po zakřivené dráze. Z těch samých důvodů také jeho hodiny tikají s nezměněnou frekvencí po celou dobu letu a jeho čas plyne rovnoměrně.V souřadnicích spojených s fotonem je let fotonu přímočarý s konstantní rychlostí c_o světla ve vakuu. V těchto souřadnicích se let fotonu jeví jako pohyb po přímce mezi hvězdou a Zemi bez přítomnosti Slunce.

Smysl jednotlivých diagramů hlouběji pochopíme, když uvedeme detaily jejich výpočtu (digitální intrgrace Obr. 4). Postupuje se po krocích elementárního času Δt pozemních hodin. V podstatě zopakujeme to, co jsme již uvedli v souvislosti s fotonem.

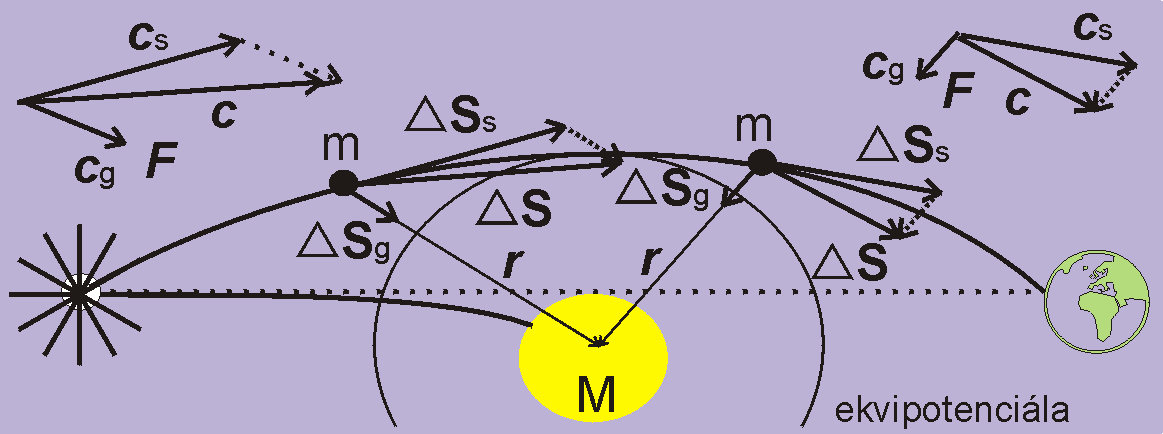
Obr. 4  K vysvětlení animace programem – geodetika.exe

Vlivem gravitační síly Slunce se rychlost fotonu mění co do velikosti a směru. V každém časovém úseku Δt se rychlost skládá z vektorového součtu dvou složek: ze setrvační rychlosti Cs, kterou foton nabyl v předešlém časovém úseku Δt, a z gravitační rychlosti Cg = a Δt, kterou foton nabude vlivem gravitační síly F ve stávajícím časovém úseku Δt, přičemž a je zrychlení vyvolané sílou F. Rychlost fotonu C v daném úseku Δt je daná vektorovým součtem C = Cs + Cg, a přírůstek trajektorie je pak ΔS = C Δt.

Změna rychlosti fotonu – zrychlení – je v každém časovém úseku úměrná rozdílu rychlosti C na konci minulého a na konci stávajícího úseku: a = ΔC /Δt. Je to prostě numerická derivace rychlosti, jak je v kinetice zrychlení definováno.

Když Slunce nebrání přímému vidění hvězdy ze Země, můžeme pozorovat spektrum jejího světla. V přítomnosti gravitačního pole Slunce se spektrum posune směrem k vyšším – modrým frekvencím spektra. Tento posun spektra Einstein předpověděl a vypočítal ještě v době, když jeho existence vlivem Slunce nebyla prokázána pro jeho nepatrnost. Nicméně, na experimentální ověření existence posuvu spektra Einstein vsadil udržitelnost své teorie když ([1], str. 178) psal: „Kdyby posunutí červených spektrálních čar vlivem gravitačního potenciálu neexistovalo, byla by obecná theorie relativity neudržitelná„.

Podle grafu na Obr. 2 je kmitočet (barva) fotonu při dopadu na Zemi vyšší než je odpovídající frekvence bez přítomnosti gravitace Slunce. Zakřivení trajektorie a času nezávisí na kmitočtu a tudíž posuv směrem k modré barvě spektrálních čar je stejný pro všechny frekvence:

Pozorovat červený posuv při zatmění Slunce se nedaří pro jeho obtížnost a nepatrnost. Experimentálně prokázat existenci posuvu spektrálních čar se povedlo teprve v roce 1960, tentokrát vlivem gravitačního pole Země. Experimenty prováděli Robert Pound a Glen Rebka na Harvardské univerzitě. Přístroje umístili ve věži, přičemž vzdálenost mezi vysílačem a přijímačem záření byla 22,55 metru. Když byl vysílač umístěn níž, pozorovali posun frekvence přijímaného záření směrem k nižším frekvencím (červený posuv). V opačné poloze (přijímač níž), kdy se záření šířilo shora dolů, pozorovali posuv frekvence směrem k vyšším frekvencím (modrý posuv). Bez započítání posuvu frekvence záření vlivem gravitačního pole by nebyly přesné ani družicové navigační systémy typu GPS.

Červený posuv v pozemských podmínkách brilantně ilustruje Obr.5 [4]. Ukazuje, jak se mění kmitočet fotonu (červený posuv), když jeho vzdálenost r od centra Země narůstá. Kmitočet f a tudíž i vlastní energie fotonu W_f = hf tak klesá. Tento pokles energie je však vykompenzovaný narůstající potenciální energii Wp a princip zachování energie je naplněn.

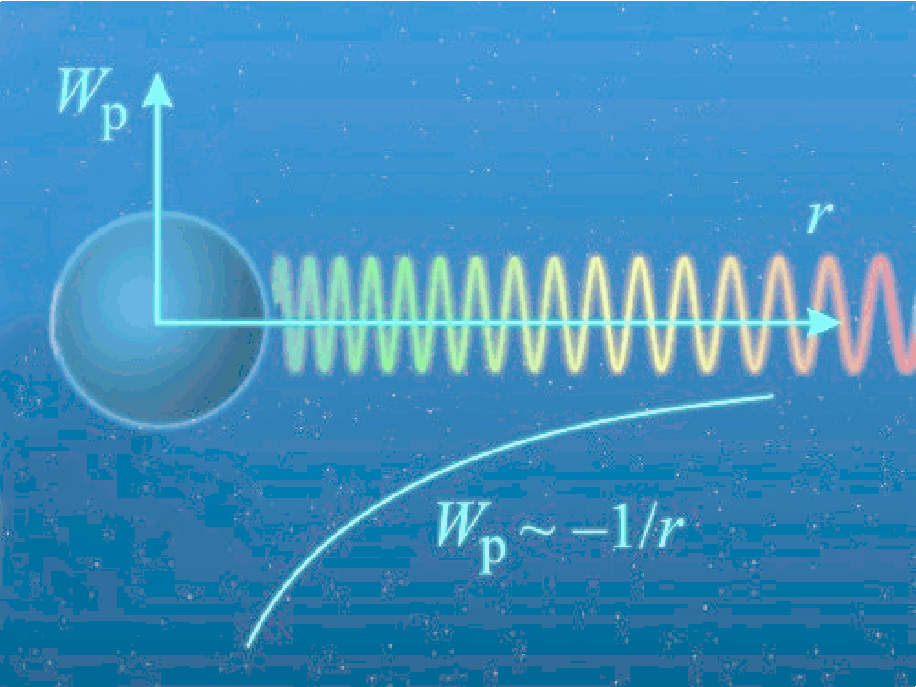
Obr. 5  Vliv gravitace Země na kmitočet fotonu při jeho stoupání vzhůru – cerveny-posuv.exe

Foton je chameleón, který mění svou barvu (kmitočet f) tak, aby součet gravitační Wp, kinetické Wk a vlastní energie W_f fotonu zůstal nezměněný: Wp + Wk + W_f = konstanta.

Konfrontujme nyní výsledky pozemního experimentu ilustrované grafem Obr. 5 s výsledky výpočtů zobrazené grafy na Obr. 2. V pozemním experimentu je přijímač záření umístěn výš a tudíž v místě menší gravitační síly (větší potenciální energie fotonu). Analogicky je v grafech na Obr. 2 jeho potenciální energie na začátku a konci jeho dráhy větší než v blízkosti Slunce.

V místě přijímače a vysílače hodiny fotonu vyhodnocují čas počtem period záření (kmitočtem fotonu) v souladu s definicí výše citované SI jednotky času. Podle grafu Obr. 5, v místě vysílače tikají hodiny fotonu rychleji než v místě výše položeného přijímače, pro který to znamená prodloužení – dilatace času fotonu vlivem jeho narůstající potenciální energie. Koresponduje to s grafem frekvence fotonu na Obr. 2 v blízkosti a dál od Slunce.

Kromě výše diskutovaného gravitačního posuvu spektra známe také kosmologický rudý posuv spektra, který při pozorovaní velmi vzdálených kosmických objektů (galaxii) poprvé zaznamenal a popsal v roce 1924 astronom Edwin Hubble [7]. Zjistil, že jejich spektrální čáry jsou posunuty směrem k dlouhovlnovému (červenému) konci spektra oproti slunečnímu spektru. Tento úkaz se vysvětluje pomocí Dopplerova jevu, dobře známému i z každodenního života. Jestliže se sanitka vzdaluje od nás rychlostí v, a její siréna vysílá signál s frekvencí f_o, pak stojící pozorovatel ho slyší s nižší frekvencí f. Ilustruje to Obr. 6, kde zdroj vlnění je znázorněn hodinami fotonu.

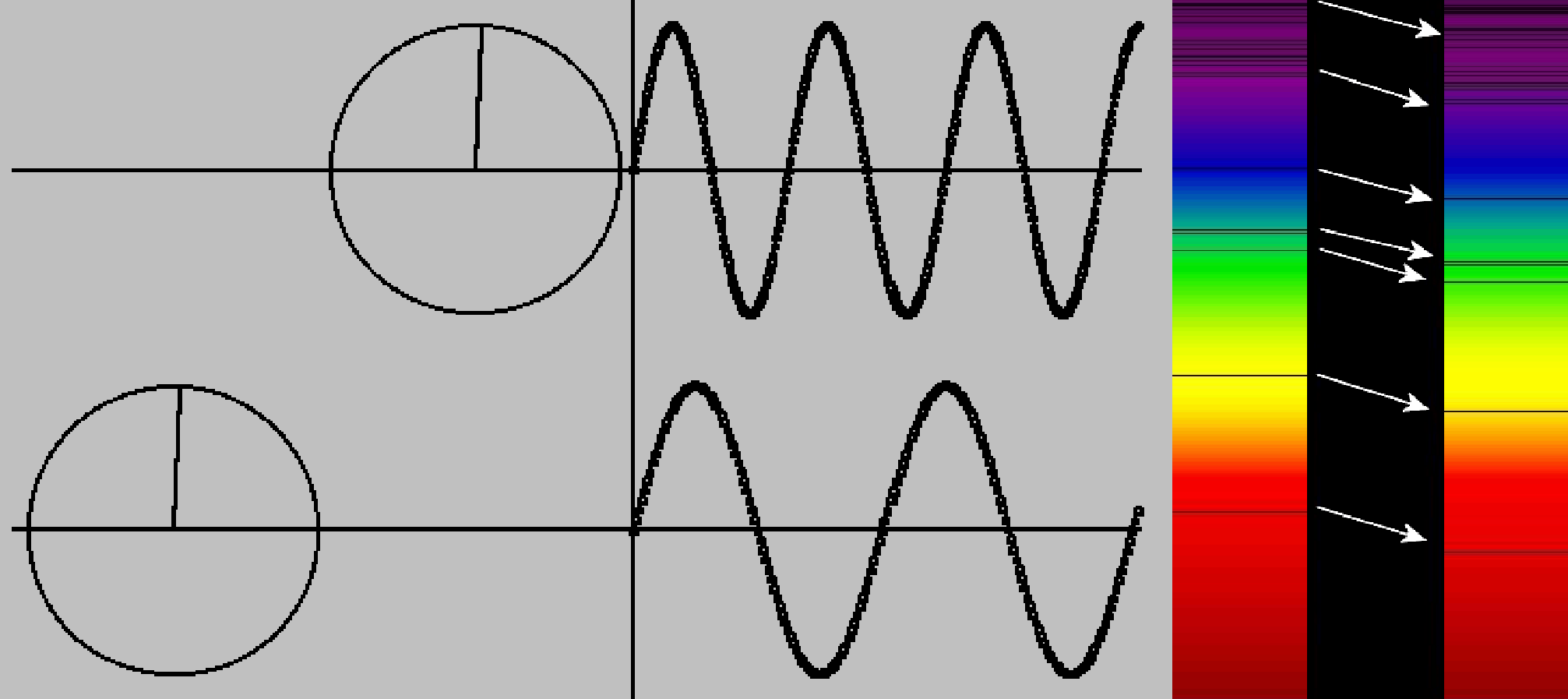
Obr. 6  Dopplerův jev (doppleruv-jev.exe) a rudý posuv spektra galaxie

Z elementární analýzy Dopplerova jevu vyplývá, že rozdíl (f_o – f) kmitočtu spektrální čáry slunečního světla resp. galaxie činí Δf = f_o×v/c_o, kde c_o je rychlost světla ve vakuu. Odtud snadno vypočítáme, že galaxie se od nás vzdaluje rychlostí v. Později Hubble objevil, že tento posuv je tím větší čím větší je vzdálenost galaxie od nás. Například galaxie Hydra se vzdaluje rychlostí 11 000 km/s a Panna rychlostí 1200 km/s. To nakonec vedlo k teorii rozpínání vesmíru.

Slunce je relativně malá hvězda, jejíž působení na světlo gravitačním polem lze detekovat jen sofistikovanými experimenty. Ve vesmíru existují natolik hmotné objekty, že svou gravitací jsou schopny pohltit ve své blízkosti každý objekt včetně světla cizích hvězd a dokonce své vlastní fotony. Jelikož každý foton, který se pokusí opustit tento objekt, je vtáhnout zpět a tudíž nemůže k nám na Zemi přinést informaci. Astronomové takový objekt nazvali černou dírou.

Termín černá díra zavedl John Wheeler teprve v roce 1967 [5], ačkoliv o existenci těchto vesmírných objektů se uvažovalo již od Newtonových časů. Objevit první černou díru se podařilo teprve v roce 1971. Obr. 7 ilustruje jak se foton „snaží“ opustit černou díru všemi směry, ta ho však svou gravitační silou donutí vrátit se spět.

Obr. 7  Černá díra „pohltí“ své vlastní fotony – cerna-dira.exe

Na pravé straně Obr. 7 je znázorněn diagram rychlosti fotonu, který opustil černou díru směrem kolmým na její povrch. Jeho počáteční rychlost se zpomaluje až do nuly a pak se foton „poslušně“ se zrychlením vrací opačným směrem a zapadne do černé díry stejnou rychlostí, jakou ji opustil. Stoupání trvá tak dlouho, dokud se celá konetická energie Wk fotonu nepromění v potenciální energii Wp. Analogicky se chová kámen hmotnosti m hozený vzhůru rychlostí v. Jeho počáteční kinetická energie E = mv²/2 se mění v potenciální, a když rychlost dosáhne hodnoty v = 0, kámen začne padat zpět. Pozor ať Vám nespadne na hlavu.

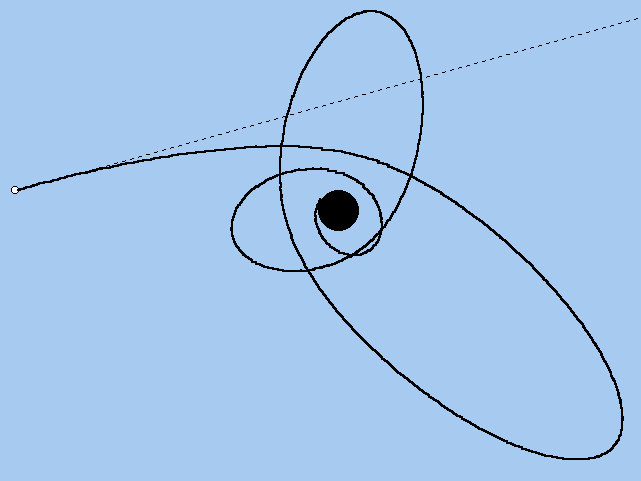
Obr. 8  Černá díra „pohltí“ fotony hvězdy – foton-cerna-dira.exe

Černá díra pohltí vše, co se vyskytne v dosahu její gravitačního pole a nemá dostatečnou rychlost, aby uniklo. Obr. 8 znázorňuje trajektorii fotonů, jak nakonec po spirálovité dráze zapadne do černé díry. Ten samý foton by Slunce odklonilo jen nepatrně, jak to ilustruje Obr. 2.

K odvození grafů na Obr. 2 nám posloužil Newtonův gravitační zákon, který vyjadřuje gravitační sílu F působící na hmotnost m. Je zvykem tuto hmotnost nazývat tíhová (gravitační) hmotnost. Použili jsme také Newtonův zákon síly F = ma, kde a je zrychlení hmotnosti m pod působením síly F. V tomto případě se hmotnost m občas nazývá setrvační (inerciální) hmotnost. Přívlastky hmotnosti mají zdůraznit, že se jedná o veličinu, která vystupuje ve dvou odlišných pohledech na fyzikální jev, jejichž společním jmenovatelem je síla F.

Od dob Newtona se badatelé pokoušeli dokázat, že v obou pohledech se jedná o jednu a tutéž hmotnost. Přesvědčivě to dokázal až Lorand Eötvös svýma pokusy, které prováděl pomocí torzních vah. Resultáty publikoval v r. 1890 [6]. Tyto a následné experimentální výsledky o rovnosti gravitační a setrvační hmotnosti stimulovaly myšlenku, že gravitační sílu lze chápat také jako důsledek zrychlení pokud se hmotnost m pohybuje v speciálním prostoru, který Einstein nazval zakřivený časoprostor. V tomto prostoru lze pohyb popisovat jen v pojmech dynamiky: čas, rychlost v, zrychlení a, kinetická energie Wk = mv²/2, bez potřeby zavádět pojem gravitace (přitažlivost).

V povaze myšlení člověka je přirovnávat neviditelné objekty (fotony) k věcem známým z každodenního života (hodiny) a těžko pochopitelné přírodní jevy vysvětlovat pomocí vymyšlených vědecko-fantastických (Sci-Fi) příběhů. Gravitace jako důsledek zrychleného pohybu se s oblibou znázorňuje výtahem, v kterém člověk pociťuje tíhu, když výtah stojí. Okamžitě přestane tíhu vnímat, když se výtah utrhne a s rovnoměrně zrychleným pohybem začne padat. Ztrátu tíhy lze si vysvětlit tím, že gravitace z nějakých důvodů zmizela. Opačně, kdyby se výtah dal do po hybu vzhůru rovnoměrně zrychleným pohybem, člověk by pocítil větší tíhu a mohl by si myslet, že stoupla gravitace – přitažlivost Země.

Grafy na Obr. 2 lze také popsat toliko v pojmech dynamiky pomocí následujícího Sci-Fi scénáře.

Začátek Sci-Fi scénáře

Postavíme dálnici mezi hvězdou a Zemí, která má zakřivení přesně takové jako trajektorie fotonu, kterou jsme zaznamenali ze Země (Obr. 2). Po dostavbě odstraníme Slunce s jeho gravitací a zůstane jen dálnice, po které pojede známý pilot formule 1. Hvězda ani Země nemají žádné gravitační pole a pilot se svým autem se drží dálnici jen díky důmyslným bezpečnostním pásům, které nekladou pohybu žádný odpor.

Auto vybavíme hodinami stejné konstrukce jakými smě měřili trajektorii fotonu. Do auta umístíme váhy, které při každém tiknutí hodin zaregistrují hodnotu a směr přetížení auta při jízdě po zakřivené dálnici. Auto je poháněné elektromotorem, který je napájený z akumulátoru. Je to potenciální energie auta (obdoba potenciální energie fotonu). Pilot startuje se 100% nabitým akumulátorem a navíc na startu ho obsluha postrčí a tím mu ještě přidá kinetickou energii.

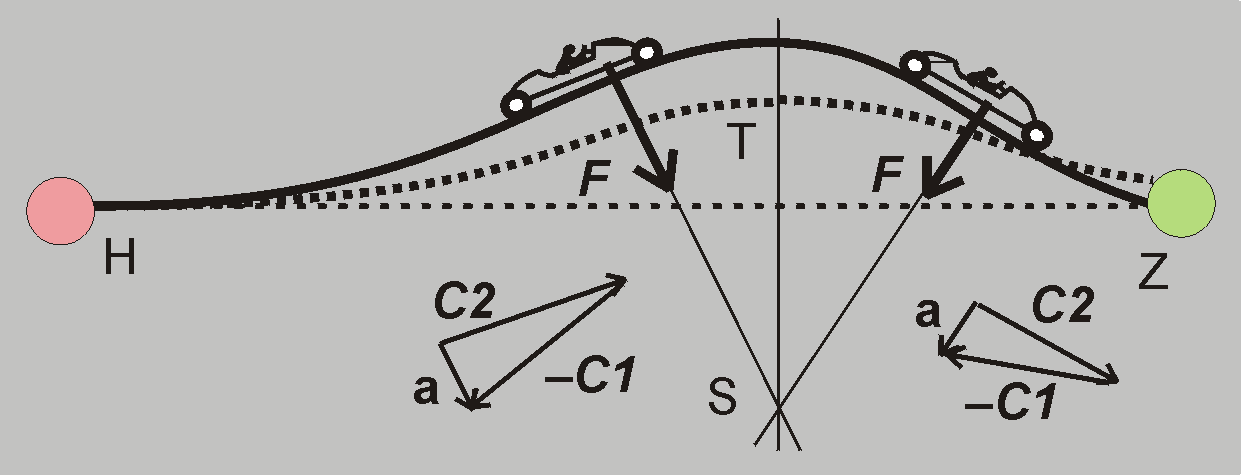
Pilot dostal graf profilu dálnice a graf času T, podle kterých má trasu projet. Je to pro něho jistý rébus: jakou rychlostí má jet? Naštěstí ve škole se dobře učil a měl skvělého učitele matematiky, který ho naučil dokonce vektorovou algebru. Pro danou elementární změnu času Δt z grafu trasy odměřil délku ujeté dráhy a tak zjistil vektor rychlosti C1, přičemž jeho směr je dán daným místem dráhy. Výpočet opakoval pro sousední elementární časový úsek Δt, kde rychlost vycházela C2. Vektorový rozdíl vydělený časovým rozdílem mu dal hodnotu zrychlení auta a = (C2 – C1)/Δt, kterou když vynásobil hmotností m auta získal vektor přetížení F.

Má-li pilot dodržet vypočítanou rychlost jízdy, auto musí zpočátku čerpat energii z akumulátoru, čím jeho potenciální energie klesá, ale zato stoupá jeho rychlost a kinetická energie. Po jisté době pilot zjistí, že musí „plyn“ ubírat a dokonce začat brzdit, aby dodržel vypočítané zpomalení rychlosti. Brzdí motorem, a jeho dokonalý motor mění kinetickou energii na elektrickou a nabíjí akumulátor. Nakonec pilot dojede do cíle s větší rychlostí, než jakou ho postrčili při startu, a jeho akumulátor je vybitý jen minimálně.

Zrychlený pohyb auta zaznamenávají váhy jako přetížení F. Díky speciálnímu tvaru dálnice a vypočítanému grafikonu rychlosti jízdy se prodloužené přímky vektorů F kříží v jednom bodě S. Pilot je rád, že jím vypočítané přetížení se shoduje se záznamy váhy.

Pilot formule 1 v Sci-Fi scénáři vypočítal požadovanou rychlost a zrychlení auta ze zadaného zakřivení dálnice a časového diagramu jízdy. Postupoval přitom po krocích v opačném sledu, než jsou uvedeny u výkladu Obr. 4, který se opíral o gravitaci Slunce. V popsaném scénáři jsme mluvili o zrychlení a přetížení aniž bychom vyslovili slovo gravitaci. Dospěli jsme tak k závěru, že působení gravitace lze vykládat také v pojmech jen dynamiky (zrychlení) a geometrie (zakřivení časoprostoru). Jinými slovy [7]:

Tento poznatek, zvaný princip ekvivalence, je jeden ze dvou postulátů, na kterých stojí obecná teorie relativity. Druhý postulát zní:

Podle těchto principů obecné teorie relativity je gravitace projevem inerciální síly v zakřiveném časoprostoru.

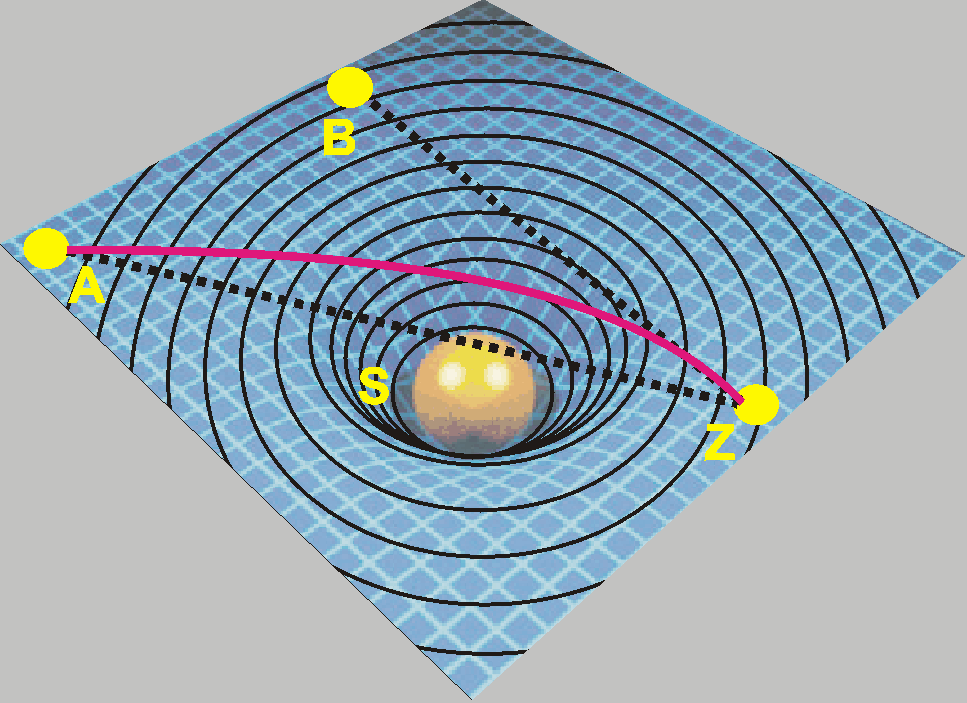
Obr. 11  Ilustrace zakřivení časoprostoru dopadovou plošinou trampolíny

Zakřivení časoprostoru ilustruje dopadová plošina trampolíny na Obr. 11. Pokud plošina není zatížená, představuje rovinou plochu a kulička hozená v bodě A se do bodu Z setrvačností dokutálí rovnoměrnou rychlostí. Koule S svou vahou zakřiví dopadovou plošinu. Oválné křivky zde představují vrstevnice potenciální energie kuličky na zakřivené ploše. Na zakřivenou plochu je třeba nyní kuličku vrhnout jiným směrem, aby se dokutálela do bodu Z po zakřivené dráze. Koule S vytvořila na plošině jamku, do které kulička zrychleným válením padá, její potenciální energie klesá, avšak díky své setrvační rychlosti dokáže jamku opustit a dopadnout do bodu Z. Směrnice dráhy v koncovém bodě míří do bodu B. Na zakřivené plošině se kulička pohybuje nerovnoměrnou rychlostí pod působením gravitačního pole Země. Kdyby gravitace neexistovala, pak by se kulička dostala z bodu A do Z po uvedené trase jen v případě, když by byla vhozena správnou počáteční rychlostí a směrem. Její okamžitá rychlost a zrychlení na trase by musela být regulovaná podle časového diagramu, jak ilustruje Obr. 2 a program casoprostor.exe, kde ovšem tou kuličkou je foton.

Při prohlížení grafu rychlosti fotonu na Obr. 2 se nejednomu hloubavému čtenáři s podivem zdvihá obočí, když vidí, že rychlost fotonu v blízkosti Slunce je větší než ve vzdáleném vzduchoprázdnu. Je přece známo, že dle speciální teorie relativity žádný objekt nemůže převýšit rychlost c₀ světla ve vakuu. Jenže foton není „obyčejný“ objekt. Foton je „stavební kámen“ světla, foton je světlo samo a speciální teorie relativity předpokládá vakuum bez přítomnosti gravitačního pole.

Mluvíme-li o rychlosti světla c₀, máme na mysli prostor bez gravitačního pole a zbaveného všech látkových prvků (atomů, molekul). Jaká je tedy rychlost světla (fotonu) v těchto podmínkách? Je to otázka, kterou si myslitelé kladli od nepaměti (…, Aristoteles, Galilei, Newton, Maxwell, Michelson …) a kladou si ji dodnes.

V roce 1983 Generální konference pro váhy a míry přijala pro soustavu SI (Système International d’Unités) základní jednotku délky (metr) definicí:
Metr je délka dráhy, kterou urazí světlo ve vakuu během časového intervalu 1/299 792 458 sekundy.

Konference tímto zároveň zafixovala rychlost světla c₀ = 299 792 458 [ms^–1] ve vakuu, a chtělo by se dodat, v nepřítomnosti gravitačního pole. K uvedené definici jednotky délky se přistoupilo, jelikož dnes umíme čas měřit s největší přesností (s nejistotou 8.10^–15) ze všech měření fyzikálních veličin.
Jenže zafixovaná rychlost není ta, kterou naměříme s přístroji. Rychlost c je definovaná jako podíl ujeté délky trasy Δd za dobu Δt: c = Δd / Δt. Přesnost měření rychlosti se v průběhu dějin zvětšovala současně se zdokonalováním měřicích přístrojů. Jelikož měrná jednotka délky je dána výše uvedenou definicí Metru, zbývá už jen definovat základní měrnou jednotku času – sekundu.

Čas se odjakživa měřil hodinami založenými na periodicky se opakujícím jevu: oběh Země kolem Slunce, rotace Země kolem své osy, kmity kyvadla stařičkých hodin zvaných pendlovky atd. Dnes nejpřesnější jsou atomové hodiny, s kterými lze stanovit hodnotu sekundy s výše uvedenou mírou nejistoty. Jenže i tyto nejpřesnější hodiny podléhají vlivu gravitace, což znamená, že v okolí zemského povrchu se frekvence hodin a tedy i realizovaná sekunda SI mění s nadmořskou výškou, a to přibližně o 1,1×10^–16 na jeden metr výšky. V silnějším gravitačním poli bude sekunda delší a atomové hodiny půjdou pomaleji [3].

Vraťme se nyní ke grafu rychlosti na Obr. 2 a představme si, že chceme měřit rychlost fotonu pomocí přístrojů umístěnými v blízkosti letícího fotonu u Slunce. Pro měření fotonem přeletěné délky Δd máme k dispozici metr podle výše uvedené SI definice. Pro měření doby přeletu Δt máme k dispozici atomové hodiny. Jelikož se hodiny nacházejí v silném gravitačním poli Slunce, hodiny tikají pomaleji a ukážou menší hodnotu Δt. V důsledku toho naměříme vyšší rychlost fotonu c = Δd / Δt než je jeho rychlost c₀ v slabém, nebo v nepřítomném gravitačním poli, jak to ukazuje graf rychlosti na Obr. 2.

Atomové hodiny v blízkosti Slunce „tikají“ pomaleji, ale hodiny fotonu zde „tikají“ rychleji jak to znázorňuje graf rozdílu času hodin fotonu a Země na Obr. 2. Není v tom rozpor, jelikož každé hodiny, které realizují sekundu SI podle definice, ve skutečnosti vytvářejí svůj vlastní čas. Změnu rychlosti chodu hodin fotonu vlivem gravitace lze indikovat jenom pomocí posuvu spektrálních čar světla. Posuv spektrálních čar v gravitačním poli Země byl potvrzen experimentálně v roce 1960 [4]. Výsledky těchto experimentů konfrontujeme s grafy na Obr. 2 v kapitole Červený/modrý posuv spektra.