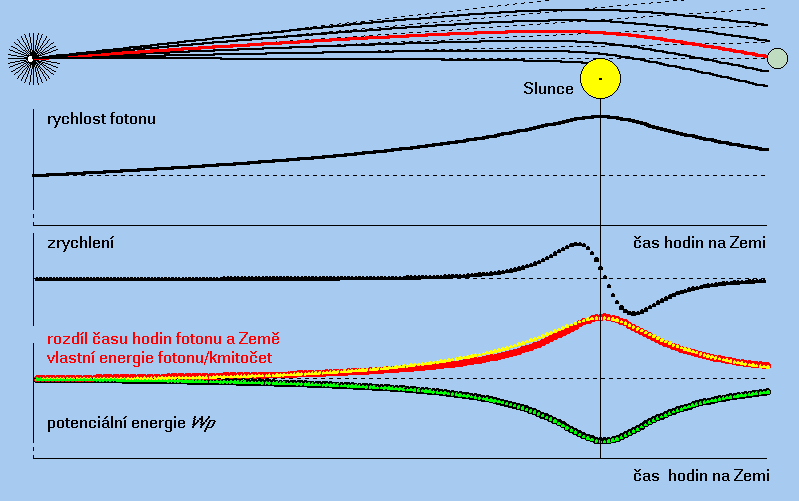
Zakřivení časoprostoru ilustruje Obr. 2 tak, jak byl vypočítán programem casoprostor.exe. Gravitační pole hvězdy a Země zanedbáváme – hmotnost Země je nepatrná oproti hmotnosti Slunce a hvězda je příliš daleko. Foton se k Slunci blíží rychlostí světla ve vakuu. Na Obr. 2 vidíme čtyři diagramy, jejichž měřítka mají ilustrativní velikost s cílem zdůraznit daný jev.

• Horní diagram znázorňuje trajektorie fotonů (paprsky světla) při svém letu poté co byly vyslány hvězdou. Jedna trasa končí na Zemi a foton přináší nám správu o existenci hvězdy. Jiné fotony na svých trasách dopadnou na Slunce, nebo nás minou. Přímka kreslená přerušovanou čarou znázorňuje trajektorii, kterou by se foton pohyboval, kdyby ho neovlivňovalo Slunce svým postavením.
• Druhý diagram ukazuje, jak se měnila rychlost letu fotonu, který dopadl na Zemi vlivem gravitace Slunce viděno ze Země a měřeno časem na Zemi. Čárkovaná přímka znázorňuje trasu fotonu letícího konstantní rychlostí, když nepůsobila gravitace Slunce. Hvězda je daleko od slunce a foton se blíží k Slunci z prostředí vakua bez gravitace rychlostí c_o. Při animaci můžeme proto vycházet z toho, že foton touto rychlostí opustil i hvězdu. Jak se blíži k Slunci, které ho přitahuje, jeho rychlost narůstá.V poslední fázi letu se foton vzdaluje od Slunce a jeho rychlost se snižuje opět vlivem přitažlivosti Slunce, ale dřív než dosáhne rychlost c_o dopadne na Zemi. Fotony, které minuli Zemi, pokračují v letu a po gigantické spirálovité dráze by dopadly na Slunce, pokud by je nepohltila nějaká černá díra jak to ilustruje Obr. 8.
• Třetí diagram znázorňuje zrychlení letu fotonu pod působením gravitace Slunce. Po dosažení maximálního zrychlení v blízkosti Slunce, zrychlení začíná klesat a dosáhne nulovou hodnotu. Stane se tak tehdy, když se foton díky své rychlosti pohybuje v konstantní vzdálenosti od Slunce po ekvipotenciále gravitace (Obr. 4). Jakmile se foton začne vzdalovat od Slunce, a vymaňuje se z působení jeho gravitace, let fotonu se zpomaluje, ale jeho rychlost je stále vyšší než c_o jakou se z dálav přiblížil k Slunci.
• Na spodním diagramu (černá křivka) je uveden graf potenciální energie fotonu, který je úměrný reciproké vzdálenosti okamžité polohy fotonu vzhledem k slunci Wp ≈ –1/r. Pokud se zdá podivné, že v blízkosti Slunce se potenciální energie fotonu zmenšuje, pak to není nic mimořádného. S tímto zdánlivě paradoxním tvrzením se spřátelíme, když si uvědomíme, že každý objekt, v tom čísle i foton, má tím menší potenciální energii, čím v silnějším gravitačním poli se nachází. Pozorujeme to a využíváme to také v každodenním životě. Voda v přehradní nádrži má větší potenciální energii než pod přehradou, přestože zde je blíž k centru Země a je přitahována větší silou. Rozdíl potenciálních energii se v hydroelektrárně promění v elektřinu.
• Žlutá křivka na spodním diagramu představuje kinetickou energii Wk vypočítanou jako kvadrát rychlosti fotonu. Červená křivka znázorňuje rozdíl plynutí času hodin fotonu a Země. Hodiny fotonu tikají rychlostí úměrnou jeho kmitočtu f, a tudíž červená křivka zobrazuje také jeho vlastní energii W_f. Je to křivka vyplývající z konstantnosti součtu tří forem energie ΔW_f = –(ΔWp + ΔWk) podle teorie uvedené v článku Foton. Čárkovaná linie představuje nulovou hodnotu (největší možnou) potenciální energii fotonu a současně kinetickou a vlastní energii/kmitočet fotonu když je tento ještě daleko od působení gravitace Slunce.

Obr. 2  Animace zakřivení časoprostoru – casoprostor.exe

Pohyb každého objektu se odehrává v čtyřrozměrném prostoru, který lze popsat třemi prostorovými souřadnicemi x, y, z a čtvrtou souřadnici času t. Graf trajektorie na Obr. 2 popisující pohyb fotonu v prostoru je jen průmět dráhy fotonu na rovinu x, y třídimenzionálního grafu Obr. 3, kde třetí rozměr je čas t. Čárkované linie znázorňují grafický postup konstrukci dráhy letu fotonu v časoprostoru. Je to na zakřivené ploše nejkratší spojnice mezi dvěma body , které se říká geodetika. Na ose x a t je rovnoměrná stupnice podle času pozemních hodin. Na ose t je vynesen také průběh času fotonu – přesněji rozdíl času na hodinách fotonu a pozemních.

Obr. 3  Náčrt konstrukce geodetiky – geodetika.exe

Geodetika je trajektorie, pro níž má minimální hodnotu tzv. integrál akce A, který je definován jako časový integrál rozdílu diference kinetické a diference potenciální energie po trase od zdroje k Zemi: A = ∫(ΔWk – Wp)dt = minimum. To znamená, že po každé jiné trase by uvedený integrál měl větší hodnotu. V článku Foton jsme uvedli, že součet diferencí vlastni a gravitační energie, jakožto i součet všech tří forem energie je rovný nule. Z toho lze odvodit, že integrál ∫ΔW_fdt = minimum. Žlutá plocha na Obr. 3 ilustruje tuto minimální hodnotu. Integrální hodnota diferencí vlastní energie fotonu vypovídá, že se frekvence fotonu během jeho letu v gravitačním poli Slunce zvýší o hodnotu úměrnou uvedenému minimu. Znamená to, že na Zemi pozorujeme posunutí spektrálních čar směrem k vyšším frekvencím – tzv. modrý posuv, o kterém bude ještě řeč v dalším článku. Poznamenejme, že stejný integrál akce A vykazuje také geodetika hozeného kamene mezi začátkem a jeho dopadem na Zemi, jelikož se jedná o jeden a ten samý princip dynamiky.

Geodetika na Obr. 3 znázorňuje let fotonu v časoprostorových souřadnicích spojených se Zemi. Můžeme spekulovat, jak vypadá trajektorie znázorněná v souřadnicích spražených s fotonem, který „nepociťuje“ přitažlivou sílu slunce, jelikož ta je vykompenzovaná odstředivou silou pohybu po zakřivené dráze. Z těch samých důvodů také jeho hodiny tikají s nezměněnou frekvencí po celou dobu letu a jeho čas plyne rovnoměrně.V souřadnicích spojených s fotonem je let fotonu přímočarý s konstantní rychlostí c_o světla ve vakuu. V těchto souřadnicích se let fotonu jeví jako pohyb po přímce mezi hvězdou a Zemi bez přítomnosti Slunce.

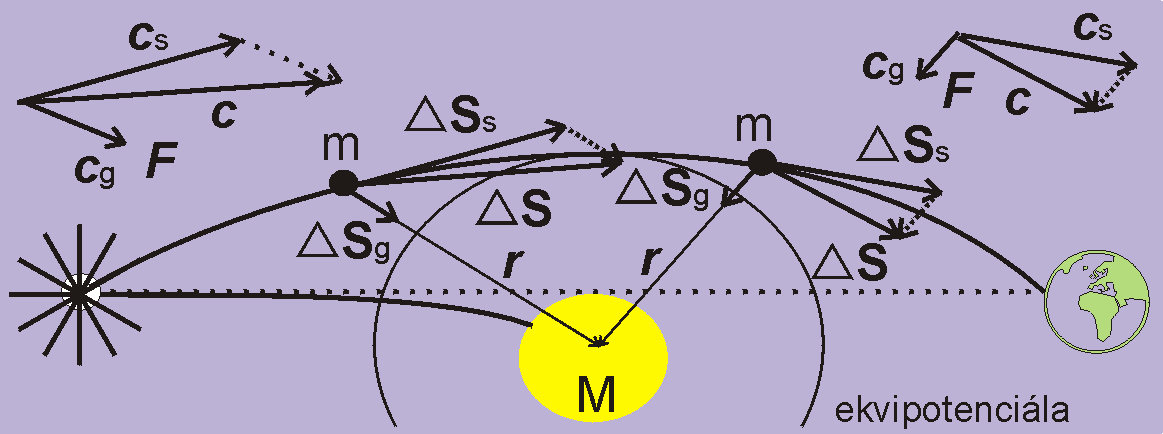
Smysl jednotlivých diagramů hlouběji pochopíme, když uvedeme detaily jejich výpočtu (digitální intrgrace Obr. 4). Postupuje se po krocích elementárního času Δt pozemních hodin. V podstatě zopakujeme to, co jsme již uvedli v souvislosti s fotonem.

Obr. 4  K vysvětlení animace programem – geodetika.exe

Vlivem gravitační síly Slunce se rychlost fotonu mění co do velikosti a směru. V každém časovém úseku Δt se rychlost skládá z vektorového součtu dvou složek: ze setrvační rychlosti Cs, kterou foton nabyl v předešlém časovém úseku Δt, a z gravitační rychlosti Cg = a Δt, kterou foton nabude vlivem gravitační síly F ve stávajícím časovém úseku Δt, přičemž a je zrychlení vyvolané sílou F. Rychlost fotonu C v daném úseku Δt je daná vektorovým součtem C = Cs + Cg, a přírůstek trajektorie je pak ΔS = C Δt.

Změna rychlosti fotonu – zrychlení – je v každém časovém úseku úměrná rozdílu rychlosti C na konci minulého a na konci stávajícího úseku: a = ΔC /Δt. Je to prostě numerická derivace rychlosti, jak je v kinetice zrychlení definováno.