K odvození grafů na Obr. 2 nám posloužil Newtonův gravitační zákon, který vyjadřuje gravitační sílu F působící na hmotnost m. Je zvykem tuto hmotnost nazývat tíhová (gravitační) hmotnost. Použili jsme také Newtonův zákon síly F = ma, kde a je zrychlení hmotnosti m pod působením síly F. V tomto případě se hmotnost m občas nazývá setrvační (inerciální) hmotnost. Přívlastky hmotnosti mají zdůraznit, že se jedná o veličinu, která vystupuje ve dvou odlišných pohledech na fyzikální jev, jejichž společním jmenovatelem je síla F.

Od dob Newtona se badatelé pokoušeli dokázat, že v obou pohledech se jedná o jednu a tutéž hmotnost. Přesvědčivě to dokázal až Lorand Eötvös svýma pokusy, které prováděl pomocí torzních vah. Resultáty publikoval v r. 1890 [6]. Tyto a následné experimentální výsledky o rovnosti gravitační a setrvační hmotnosti stimulovaly myšlenku, že gravitační sílu lze chápat také jako důsledek zrychlení pokud se hmotnost m pohybuje v speciálním prostoru, který Einstein nazval zakřivený časoprostor. V tomto prostoru lze pohyb popisovat jen v pojmech dynamiky: čas, rychlost v, zrychlení a, kinetická energie Wk = mv²/2, bez potřeby zavádět pojem gravitace (přitažlivost).

V povaze myšlení člověka je přirovnávat neviditelné objekty (fotony) k věcem známým z každodenního života (hodiny) a těžko pochopitelné přírodní jevy vysvětlovat pomocí vymyšlených vědecko-fantastických (Sci-Fi) příběhů. Gravitace jako důsledek zrychleného pohybu se s oblibou znázorňuje výtahem, v kterém člověk pociťuje tíhu, když výtah stojí. Okamžitě přestane tíhu vnímat, když se výtah utrhne a s rovnoměrně zrychleným pohybem začne padat. Ztrátu tíhy lze si vysvětlit tím, že gravitace z nějakých důvodů zmizela. Opačně, kdyby se výtah dal do po hybu vzhůru rovnoměrně zrychleným pohybem, člověk by pocítil větší tíhu a mohl by si myslet, že stoupla gravitace – přitažlivost Země.

Grafy na Obr. 2 lze také popsat toliko v pojmech dynamiky pomocí následujícího Sci-Fi scénáře.

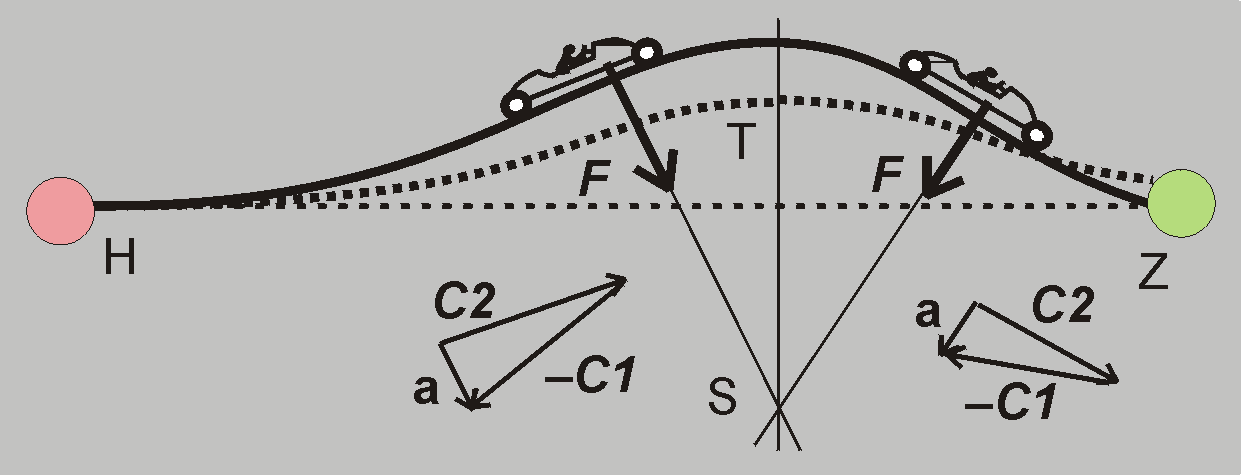
Začátek Sci-Fi scénáře

Postavíme dálnici mezi hvězdou a Zemí, která má zakřivení přesně takové jako trajektorie fotonu, kterou jsme zaznamenali ze Země (Obr. 2). Po dostavbě odstraníme Slunce s jeho gravitací a zůstane jen dálnice, po které pojede známý pilot formule 1. Hvězda ani Země nemají žádné gravitační pole a pilot se svým autem se drží dálnici jen díky důmyslným bezpečnostním pásům, které nekladou pohybu žádný odpor.

Auto vybavíme hodinami stejné konstrukce jakými smě měřili trajektorii fotonu. Do auta umístíme váhy, které při každém tiknutí hodin zaregistrují hodnotu a směr přetížení auta při jízdě po zakřivené dálnici. Auto je poháněné elektromotorem, který je napájený z akumulátoru. Je to potenciální energie auta (obdoba potenciální energie fotonu). Pilot startuje se 100% nabitým akumulátorem a navíc na startu ho obsluha postrčí a tím mu ještě přidá kinetickou energii.

Pilot dostal graf profilu dálnice a graf času T, podle kterých má trasu projet. Je to pro něho jistý rébus: jakou rychlostí má jet? Naštěstí ve škole se dobře učil a měl skvělého učitele matematiky, který ho naučil dokonce vektorovou algebru. Pro danou elementární změnu času Δt z grafu trasy odměřil délku ujeté dráhy a tak zjistil vektor rychlosti C1, přičemž jeho směr je dán daným místem dráhy. Výpočet opakoval pro sousední elementární časový úsek Δt, kde rychlost vycházela C2. Vektorový rozdíl vydělený časovým rozdílem mu dal hodnotu zrychlení auta a = (C2 – C1)/Δt, kterou když vynásobil hmotností m auta získal vektor přetížení F.

Má-li pilot dodržet vypočítanou rychlost jízdy, auto musí zpočátku čerpat energii z akumulátoru, čím jeho potenciální energie klesá, ale zato stoupá jeho rychlost a kinetická energie. Po jisté době pilot zjistí, že musí „plyn“ ubírat a dokonce začat brzdit, aby dodržel vypočítané zpomalení rychlosti. Brzdí motorem, a jeho dokonalý motor mění kinetickou energii na elektrickou a nabíjí akumulátor. Nakonec pilot dojede do cíle s větší rychlostí, než jakou ho postrčili při startu, a jeho akumulátor je vybitý jen minimálně.

Zrychlený pohyb auta zaznamenávají váhy jako přetížení F. Díky speciálnímu tvaru dálnice a vypočítanému grafikonu rychlosti jízdy se prodloužené přímky vektorů F kříží v jednom bodě S. Pilot je rád, že jím vypočítané přetížení se shoduje se záznamy váhy.

Pilot formule 1 v Sci-Fi scénáři vypočítal požadovanou rychlost a zrychlení auta ze zadaného zakřivení dálnice a časového diagramu jízdy. Postupoval přitom po krocích v opačném sledu, než jsou uvedeny u výkladu Obr. 4, který se opíral o gravitaci Slunce. V popsaném scénáři jsme mluvili o zrychlení a přetížení aniž bychom vyslovili slovo gravitaci. Dospěli jsme tak k závěru, že působení gravitace lze vykládat také v pojmech jen dynamiky (zrychlení) a geometrie (zakřivení časoprostoru). Jinými slovy [7]:

Tento poznatek, zvaný princip ekvivalence, je jeden ze dvou postulátů, na kterých stojí obecná teorie relativity. Druhý postulát zní:

Podle těchto principů obecné teorie relativity je gravitace projevem inerciální síly v zakřiveném časoprostoru.

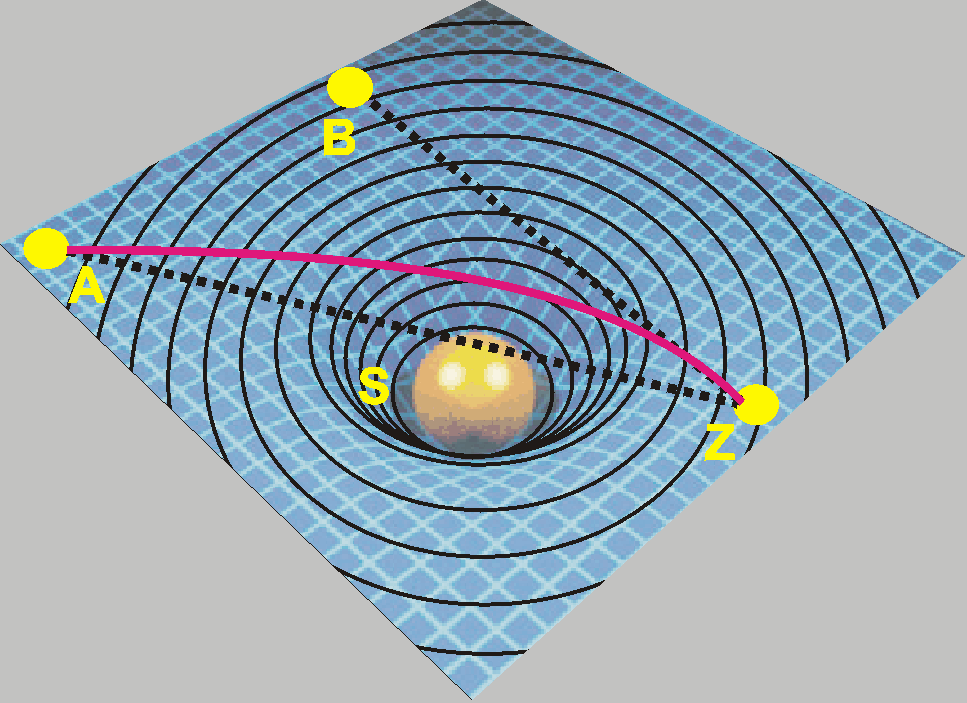
Obr. 11  Ilustrace zakřivení časoprostoru dopadovou plošinou trampolíny

Zakřivení časoprostoru ilustruje dopadová plošina trampolíny na Obr. 11. Pokud plošina není zatížená, představuje rovinou plochu a kulička hozená v bodě A se do bodu Z setrvačností dokutálí rovnoměrnou rychlostí. Koule S svou vahou zakřiví dopadovou plošinu. Oválné křivky zde představují vrstevnice potenciální energie kuličky na zakřivené ploše. Na zakřivenou plochu je třeba nyní kuličku vrhnout jiným směrem, aby se dokutálela do bodu Z po zakřivené dráze. Koule S vytvořila na plošině jamku, do které kulička zrychleným válením padá, její potenciální energie klesá, avšak díky své setrvační rychlosti dokáže jamku opustit a dopadnout do bodu Z. Směrnice dráhy v koncovém bodě míří do bodu B. Na zakřivené plošině se kulička pohybuje nerovnoměrnou rychlostí pod působením gravitačního pole Země. Kdyby gravitace neexistovala, pak by se kulička dostala z bodu A do Z po uvedené trase jen v případě, když by byla vhozena správnou počáteční rychlostí a směrem. Její okamžitá rychlost a zrychlení na trase by musela být regulovaná podle časového diagramu, jak ilustruje Obr. 2 a program casoprostor.exe, kde ovšem tou kuličkou je foton.